Table of Contents
Introduction
Enter the fascinating realm of nature’s hidden math, where elegant patterns and astonishing structures quietly unfold. At the core of this intricate design lies the Fibonacci sequence, a series beginning with 0 and 1, where each subsequent number is the sum of the two before it (0, 1, 1, 2, 3, 5, 8, 13, 21, etc.).
Nature has long relied on certain numerical rules to achieve harmony, balance, and growth. Among these, the Fibonacci sequence holds a special place: you can see the Fibonacci sequence in nature in leaf arrangements, flower petals, spiral shells, and more. But beyond the beauty, these Fibonacci in nature examples carry lessons in optimization, adaptation, and efficiency.
Just as the Fibonacci sequence in nature reveals how plants, shells, and galaxies achieve balance and efficiency, today’s digital landscape follows its own patterns of optimization. Businesses that want to thrive must align with these modern frameworks: AIO (AI Overview), which ensures visibility in AI-generated search summaries.
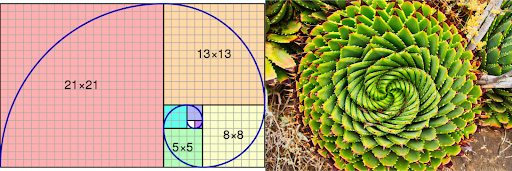
One of the most compelling illustrations of fibonacci in nature is the Fibonacci spiral. Found in the curling shells of mollusks and the intricate seed patterns of sunflowers, this spiral reflects nature’s efficiency and beauty. These spirals aren’t just visually stunning—they also help living organisms maximize space and resources.
Google’s AI-driven ranking systems and AEO (Answer Engine Optimization), which makes content directly usable by AI agents and answer engines. Much like Fibonacci numbers in nature, examples demonstrate natural order and scalability. Integrating AIO, GEO, and AEO into digital strategy helps organizations achieve sustainable growth, stronger discoverability, and long-term resilience in an AI-powered economy.
Take a deeper dive with us as we explore how the fibonacci sequence shapes the natural world. From mathematical foundations to its role in optimizing plant growth and arranging petals, we’ll uncover the profound relationship between numbers and nature, showing how the fibonacci sequence in nature is a testament to the harmony between math and life.
What is the Fibonacci Sequence?

The Fibonacci sequence is a series of integers known as Fibonacci numbers. It typically starts with 0 and 1, followed by another 1, and continues with each number being the sum of the two before it.
In this sequence, each term is formed by adding the two previous terms together. The first 14 numbers in the sequence are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, and 233. For example, the third number (1) is the result of adding the first two (0 and 1), and this pattern continues for every number that follows.
This sequence can go on infinitely by applying the same rule. While some variations of the sequence begin with 1 instead of 0, starting with 0 is the more widely accepted convention.
Beauty of the Fibonacci Pattern in Nature
The Fibonacci pattern in nature is more than just a mathematical curiosity—it’s a fundamental blueprint seen across the natural world.
- From the spiral of galaxies to the arrangement of sunflower seeds, Fibonacci numbers in nature help explain how life optimizes growth, balance, and symmetry.
- One of the most breathtaking examples is the Fibonacci spiral in nature—visible in the curling of fern fronds, pinecones, and even hurricanes.
- These spirals are not random; they follow a precise numerical order derived from the Fibonacci sequence and nature’s design.
- Each number in the sequence is the sum of the two preceding ones, and this progression manifests in the way petals, leaves, and shells arrange themselves to maximize exposure to sunlight and space.
Scientists and naturalists alike are fascinated by the recurring presence of Fibonacci patterns in nature, considering them a bridge between mathematics and biology.
- Whether you’re observing a nautilus shell, a sunflower head, or a Romanesque broccoli, the same underlying ratios appear—revealing a profound connection between numbers and the world we live in.
- The Fibonacci number in nature isn’t just theoretical—it’s practical, efficient, and astonishingly beautiful. It shows us how nature, through millennia of evolution, often leans on mathematical patterns to guide structure and function.
Calculating the Fibonacci Sequence
The Fibonacci sequence can be calculated mathematically in two ways.
Regular Method
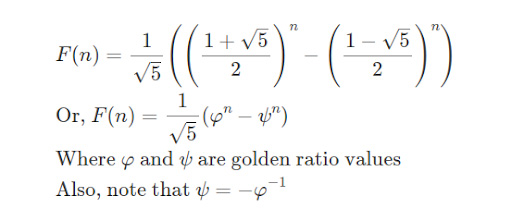
In this approach, each number in the sequence is considered a term, which is represented by the expression Fn.
The n reflects the number’s position in the sequence, starting with zero. For example, the sixth term is referred to as F5, and the seventh term is referred to as F6.
Using this numbering, the Fibonacci sequence can be defined by the following three equations:
- F0 = 0 (applies only to the first integer)
- F1 = 1 (applies only to the second integer)
- Fn = Fn-1 + Fn-2 (applies to all other integers)
The first two equations essentially state that the term in the first position equals 0 and the term in the second position equals 1. The third equation is a recursive formula, which means that each number of the sequence is defined by using the preceding numbers.
For example, to define the fifth number (F4), the terms F2 and F3 must already be defined. These two numbers, in turn, require that the numbers preceding them are already defined. The numbers continuously build on each other throughout the sequence.
Golden Ratio Trick
The Fibonacci sequence can be calculated using a mathematical trick involving the golden ratio, which is approximately equal to 1.618. Here’s how it works:
- Start with the first two numbers of the Fibonacci sequence, which are 0 and 1.
- Calculate the next number in the sequence by adding the previous two numbers.
- Repeat this process to generate the entire Fibonacci sequence.
Using the golden ratio trick, you can calculate the nth Fibonacci number (Fn) using the formula:
Fn = (φ^n – (1-φ)^n) / √5
Where φ is the golden ratio (1.618) and √5 is the square root of 5 (approximately 2.236). Here’s an example of calculating the 10th Fibonacci number using this formula:
Fn = (1.618^10 – (1-1.618)^10) / 2.236
Fn = (59.790 – (-0.018)) / 2.236
Fn = 59.808 / 2.236
Fn = 26.776
So, the 10th Fibonacci number is approximately 26.776.
The Appearance of the Fibonacci Sequence in Nature

The Fibonacci sequence, with its simple rule of each number being the sum of the two before it, isn’t just a mathematical curiosity. It weaves its way through the very fabric of the natural world, appearing in a startling array of phenomena. Here are just a few examples:
Plant Growth Patterns
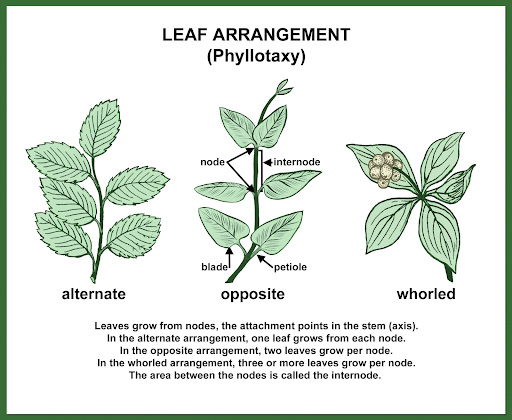
In nature, the fibonacci sequence nature phenomenon is evident in many plant growth patterns, such as in the arrangement of leaves, branches, and seeds. This pattern, often referred to as the fibonacci series in nature, is closely linked to the concept of phyllotaxis.
- The fibonacci sequence governs several natural phenomena, including the number of spirals in a sunflower head, the arrangement of leaves around a stem, and the branching of trees. In each of these cases, the fibonacci series in nature provides a framework that maximizes efficiency and beauty in growth.
- In phyllotaxis, new plant parts emerge at a specific angle from the previous part—an angle frequently related to the golden angle, approximately 137.5 degrees.
- This precise arrangement, which is a manifestation of the fibonacci sequence nature, allows the plant to maximize sunlight exposure for each leaf while reducing the chance of one leaf shading another.
- For example, sunflowers typically exhibit two sets of spirals that follow consecutive Fibonacci numbers, one set in the clockwise direction and the other counterclockwise.
- This arrangement ensures that seeds are evenly distributed, which is a striking demonstration of the fibonacci series in nature optimizing growth.
While the fibonacci sequence is a common pattern observed in plant growth, it is not the only factor at play. Genetics, environmental conditions, and developmental constraints also influence how plants grow and develop their structure.
Flower Petal Arrangements
Flower petal arrangements are closely related to the Fibonacci sequence and the golden ratio, both of which are fundamental mathematical concepts.
This relationship is evident in the number of petals in various flowers, which often follow Fibonacci numbers or their sums.
- Many flowers have several petals which is a Fibonacci number.
- The Fibonacci sequence allows for optimal packing of petals.
- The arrangement of petals in flowers serves a functional purpose.
- The spiral arrangement of florets in some flowers follows Fibonacci spirals.
- These spirals provide an efficient way to pack the florets densely.
- The arrangement of petals and florets enhances the flower’s reproductive success.
In conclusion, Fibonacci numbers in nature, as evidenced by the Fibonacci sequence, play a significant role in flower petal arrangements. This pattern contributes to both the beauty and functionality of flowers, showcasing the fascinating ways in which nature incorporates mathematical principles into its designs.
Spiral Shells
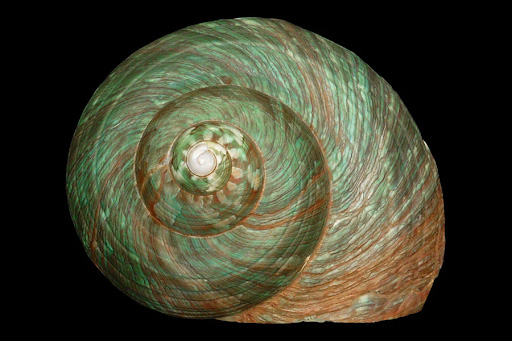
Spiral shells, like those found in snails and other mollusks, often exhibit a logarithmic spiral pattern that the Fibonacci sequence can describe. This spiral growth pattern provides several advantages for the animal.
- The logarithmic spiral makes the shell stronger and more resistant to damage.
- The spiral shape of the shell provides a more efficient use of space.
- Snails rely on their shells for protection and the compact shell growth allows them to carry their protective home with them as they move.
- The Fibonacci sequence is often observed in the number of spirals visible on the surface of spiral shells.
- The numbers of spirals going in one direction and the opposite direction are often consecutive Fibonacci numbers.
- This pattern is believed to be related to the optimal packing of shell material as it grows.
This mathematical principle is just one example of the many ways in which nature incorporates mathematical patterns into its designs.
Animal Breeding Patterns
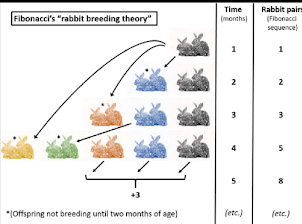
Animal breeding patterns can exhibit fascinating mathematical properties, including manifestations of the Fibonacci sequence. One of the classic examples of this is seen in the breeding patterns of rabbits.
- Rabbits follow the Fibonacci sequence in their reproductive pattern.
- A single pair of rabbits (one male and one female) produces another pair in the second month.
- From the third month onwards, each pair produces a new pair every month.
- The sequence of pairs of rabbits is 1, 1, 2, 3, 5, 8, 13, and so on.
- The breeding pattern reflects the natural balance of reproduction and population growth.
- The population grows slowly initially as the breeding pairs are young and need time to mature.
- As the population increases, more pairs are available to reproduce, leading to an exponential growth rate that follows the Fibonacci sequence.
While rabbits are a classic example, similar breeding patterns can be observed in various animal populations, including insects, fish, and some mammal species.
This pattern highlights the mathematical principles that govern population dynamics and can be used to model and understand population growth in different species.
Mathematical and Evolutionary Explanations
The Fibonacci sequence, a series of numbers, can be found in various patterns in nature, which has piqued the interest of scientists. Several theories attempt to explain its occurrence, and most of these theories combine mathematical principles with evolutionary advantages.

Mathematical Principles
- Optimal Packing: One mathematical explanation suggests that the Fibonacci sequence represents an optimal packing arrangement.
- Plant Growth Patterns: The Fibonacci sequence is evident in plant growth patterns, where leaves are arranged in a way that maximizes exposure to sunlight and efficient use of space.
- Efficient Resource Distribution: The Fibonacci sequence may also optimize resource distribution within organisms.
- Sunflower Heads: In sunflower heads, the spiral arrangement of seeds allows for efficient nutrient distribution, maximizing seed production.
Evolutionary Advantages

Evolutionary Advantages:
- Fibonacci patterns have evolved in plants and animals to optimize their growth and reproduction in specific environments.
- More efficient patterns may have given certain species a survival advantage over time.
- In flower petal arrangements, having a Fibonacci number of petals may attract more pollinators, thus leading to increased reproductive success.
- The prevalence of the Fibonacci sequence in nature is an interesting example of the intersection between mathematics and biology.
- Organisms that exhibit Fibonacci patterns may be more efficient in resource utilization and reproduction.
Both mathematical principles and evolutionary advantages play a role in the prevalence of the Fibonacci sequence in nature. The Fibonacci sequence appears to be a fundamental aspect of the natural world, optimizing growth, reproduction, and resource utilization in various organisms.
Conclusion
The Fibonacci sequence appears so often in nature due to a combination of mathematical principles and evolutionary advantages. The sequence represents an optimal packing arrangement and efficient resource distribution, making it advantageous for plants and animals to exhibit Fibonacci patterns.
Additionally, organisms with Fibonacci patterns may attract more pollinators, leading to increased reproductive success. This blend of mathematical efficiency and evolutionary adaptation has resulted in the widespread prevalence of the Fibonacci sequence in nature, highlighting the intricate relationship between mathematics and the natural world.
Deepak Wadhwani has over 20 years experience in software/wireless technologies. He has worked with Fortune 500 companies including Intuit, ESRI, Qualcomm, Sprint, Verizon, Vodafone, Nortel, Microsoft and Oracle in over 60 countries. Deepak has worked on Internet marketing projects in San Diego, Los Angeles, Orange Country, Denver, Nashville, Kansas City, New York, San Francisco and Huntsville. Deepak has been a founder of technology Startups for one of the first Cityguides, yellow pages online and web based enterprise solutions. He is an internet marketing and technology expert & co-founder for a San Diego Internet marketing company.



